| The linear buckling solver calculates the buckling load factors and
corresponding mode shapes for a structure under given loading conditions. It is
based on the assumptions that there exists a bifurcation point where the
primary and secondary loading paths intersect, and before this point is
reached, all element stresses change proportionally with the load factor. |
A linear buckling solution is obtained by solving the following eigenvalue
problem: |
|
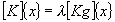
where
|
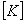Global stiffness matrix
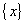Buckling mode vectors
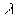Buckling load factor
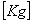Global geometric stiffness matrix
|
The geometric stiffness matrix, also known as the initial stress stiffness
matrix, is a symmetric matrix dependent on the element stress level. It
reflects the effect of geometric change on the element force vector from a
known stress state. For beam and plate bending structures, the geometric
stiffness matrix represents the stiffening effect of the tensile axial/membrane
stresses. |
The buckling solution is possible only when an existing solution is available
for determining the current stress state of the structure, which is required
for the calculation of the element geometric stiffness matrix. In Strand7, both
linear static and nonlinear static solutions can be used to as the initial
conditions for a linear buckling solution. |
The linear buckling solver performs the following steps:
|
- Calculates and assembles the element stiffness and geometric stiffness
matrices to form the global stiffness and geometric stiffness matrices. In the
stiffness calculation, material temperature dependency is considered through
the user nominated temperature case. Constraints are assembled in this process.
If the initial file is from a nonlinear solution, the stiffness matrix
calculation is based on the current material status and geometry. In other
words, a yield modulus will be used if the material has yielded and the
deformed geometry will be used if the initial solution included geometry
nonlinearity. In calculating stresses for the geometric stiffness matrix, the
solver includes any thermal strains applied in the initial solution.
- Modifies the stiffness matrix when a shift value is applied. A shift may be
used to determine modes near to a desired value.
- Solves the eigenvalue problem to get buckling load factors and the
corresponding buckling modes using the Sub-Space Iteration Method.
|
Notes
|
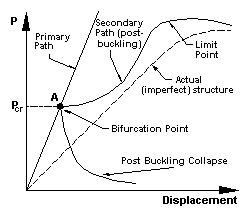
- The linear buckling analysis assumes the existence of a bifurcation point
where the primary and secondary loading paths intersect (point A in the figure
below). At this point, more than one equilibrium position is possible. The
primary path is not usually followed after loading exceeds this point and the
structure is in the post-buckling state. The slope of the secondary path at the
bifurcation point determines the nature of the post-buckling. A positive slope
indicates that the structure will have post buckling strength whilst a negative
slope means that the structure will snap through or simply collapse.
|
-
|
- Real structures have geometric and loading imperfections, often causing the
primary path curve and the bifurcation point to disappear.
|
- Another assumption for the linear buckling analysis is that the stresses in
the structure increase proportionally with the load. When the deformation is
large enough to disturb the stress distribution, linear buckling results will
no longer be valid. In this case, a nonlinear solution is more appropriate for
a realistic prediction of the structure's capacity.
|
- For real structures linear buckling analysis is best used for preliminary
design and studying the effects of various parameters. When the above
assumptions are fully or nearly satisfied, linear buckling analysis will give
accurate answers. If a more accurate estimate of the buckling load is required,
it is recommended that a nonlinear analysis be carried out so that the effect
of pre-buckling deformation can be included and the post buckling capacity
predicted.
- Combined linear static cases may also be used as initial conditions in the
linear buckling solver.
|
For more information on linear buckling analysis, see Strand7 Webnotes - Linear / Statics.
|
Menu