| The natural frequency solver is used to calculate the natural frequencies
(or free vibration frequencies) and corresponding vibration modes of an
undamped structure. The natural frequency analysis problem, is formulated as
the following eigenvalue problem: |
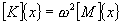 |
where
|
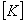 Global
stiffness matrix Global
stiffness matrix
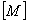 Global mass matrix Global mass matrix
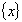 Vibration mode vector Vibration mode vector
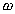 Natural (circular) frequency (radians/sec) Natural (circular) frequency (radians/sec)
|
The natural frequency solver performs the following steps: |
- Calculates and assembles the element stiffness and mass matrices to form
the global stiffness and mass matrices. In the stiffness calculation, material
temperature dependency is considered through the user nominated temperature
case. Either a consistent or lumped mass matrix can be used according to the
solver option setting. The geometric stiffness matrix will be formed and
assembled to the global stiffness matrix when an initial solution is applied.
Constraints are assembled in this process.
If the initial file is from a nonlinear solution, the stiffness and mass
matrices calculation will be based on the current material status and geometry.
More specifically, the current material modulus values will be used for
nonlinear elastic material. For plastic material, the initial modulus is used.
The current geometry is used if geometric nonlinearity is considered in the
initial solution.
-
Modifies the stiffness matrix if a shift value is applied. A shift may be
used to determine modes near to a desired value.
- Solves the eigenvalue problem to get frequencies and the
corresponding mode shapes using the Sub-Space Iteration Method.
|
Notes
|
- To help the user visualise the results, stress and strain patterns may be
generated. As the results are patterns only, only the relative magnitude is
meaningful.
- Frequency shift can be used to calculate higher modes by excluding lower
modes. A special application of the shift is in the analysis of unconstrained
structures. If the solver detects rigid body motion, a shift of -1.0 Hz is
automatically applied and a message given.
- The Sturm Sequence check is an effective method for checking the
convergence of the sub-space iteration method to ensure that the eigenvalue
solution has converged and no eigenvalues are missed.
|
For more information on natural frequency analysis, see Strand7 Webnotes - Linear / Dynamics.
|

 Menu
Menu