| Although the majority of engineering structures operate within the linear
regime and the assumptions made for the linear solution are valid, there is
however a wide class of problems which do exhibit nonlinear behaviour. The
nonlinear static solver predicts the response of structures with such
nonlinear behaviour taken into account. In Strand7, three types of
nonlinearities can be included: geometric, material and boundary nonlinearity.
|
The nonlinear static solver performs the following steps: |
- Initialises the nodal displacement vector
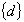 , element
stress, strain , element
stress, strain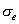 , , 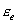 etc. etc.
- Sets the current load increment.
- Calculates and assembles the element stiffness matrices (if required),
equivalent element force vectors and external nodal force vectors. In the
stiffness calculation, material temperature dependency is considered. Depending
on whether material and/or geometric nonlinearity is considered, the current
material modulus and geometry will be used. The element geometric stiffness
matrix is also included if the corresponding option is set. Either consistent
or lumped element equivalent load vectors can be calculated according to the
option setting. Constraints are also assembled in this process and the constant
terms in the enforced displacements and shrink links are combined and applied.
At the end of this assembly procedure, the following linear equation system of
equilibrium is formed:
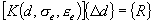
where
-
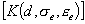 - Current
global stiffness matrix - Current
global stiffness matrix
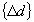 -
Displacement increment vector -
Displacement increment vector
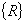 - Global
residual force vector or unbalanced force vector with - Global
residual force vector or unbalanced force vector with
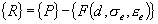
in which 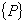 and and
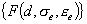
are current external force and element nodal force vectors, respectively.
- Solves the above equation for
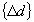
- Updates the total nodal displacement vector
- Checks convergence
displacement norm
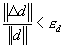
residual force norm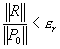
where
-
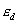 and and
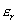 are convergence tolerance on displacement and residual force, are convergence tolerance on displacement and residual force,
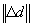 and and 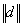 are norms of incremental and total displacement vectors,
are norms of incremental and total displacement vectors,
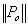 is the norm
of the residual force vector at the first iteration of each time step and is the norm
of the residual force vector at the first iteration of each time step and
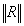 is the norm
of the residual force vector in the current iteration. is the norm
of the residual force vector in the current iteration.
- If both of the convergence criteria are satisfied, start the next load step
or stop at the last load step. If either of the criteria is not satisfied,
continue the iteration.
|
Notes
|
The Strand7 nonlinear static solver uses an algorithm based on modified
Newton-Raphson method. Major features of this algorithm are:
|
- The load increments are defined in the load increments table. In this
table, each column contains load combination factors for the corresponding load
steps or increments. For example, if the full load is applied in ten steps,
there will be ten columns in this table. In each column, combination factors
are required for the pre-defined basic load cases to determine the amount of
the load from each load case to be applied in the corresponding step.
- Multiple freedom cases may be used, with the constant terms combined using
the factors in the load increment table.
- The stiffness matrix need not be updated in every iteration. Different
strategies for global stiffness matrix updating are available:
- Update at every iteration.
- Update only in the first iteration of a load step.
- Update only in the first two iterations of a load step.
- Let the solver decide whether to update or not, based on the following
rules:
- Displacement change.
- Maximum number of iterations for no stiffness update.
- Automatic load step adjustment can be enabled to control the load increment
to achieve a better convergence rate and more importantly avoid divergence.
Before the solution is available, it is difficult to know exactly how the load
steps should be set. By using the automatic load stepping, the solver will
adjust the load based on the displacement and any divergence tendency in the
solution.
- Contact elements are considered irrespective of the type of
nonlinearity chosen in the solver panel.
- Restart can be used to continue a previously completed or aborted solution.
The restart can proceed from any of the previously saved solution steps,
provided the restart file has been saved.
|
For more information on nonlinear static analysis, see Strand7 Webnotes - Nonlinear / Statics.
|

 Menu
Menu