| << Previous (Overview) | (Nonlinear) Next >> |
ST7-R3.10 Linear |
||
|---|---|---|
| ST7-R3.10.10 Linear / Statics | ||
|
0.6 MB |
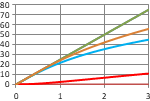
ST7-R3.10.10.1 Assumptions of Linear Analysis Linear analysis makes the following fundamental assumptions:
|
|
|
0.6 MB |
ST7-R3.10.10.2 Rigid Body Modes and Singularity Warnings in Static Solvers This Webnote examines the warning messages that can indicate rigid body motion and/or stiffness matrix singularity in a static analysis. These two concepts are not equivalent, although both can be caused by the same modelling deficiency (i.e., lack of restraint or stiffness). |
|
|
2.8 MB |
ST7-R3.10.10.3 General Model Troubleshooting Before analysis, all the data in a finite element model should be carefully checked to ensure that:
|

|
|
1.0 MB |
ST7-R3.10.10.4 Inertia Relief Inertia Relief Analysis is used whenever the applied loads are to be reacted by the inertia of the structure rather than by restrained nodes. It is a quasi-static analysis. For example, a structure such as a floating ship may be modelled without any restrained nodes. In the steady state case, the buoyancy pressure balances the weight (inertia force due to gravity). |
|
|
1.4 MB |
ST7-R3.10.10.6 Linear Buckling Analysis To gain an appreciation for performing a linear buckling analysis and interpreting the results, it is important to keep in mind the fundamental question that the linear buckling solver answers, namely: How much load is needed to excite a structural instability? The linear buckling solver can only answer this question for structures whose deformation, up to the critical load, is negligibly small. Furthermore, it cannot predict what happens to the structure when the critical load is reached or exceeded. |
|
| ST7-R3.10.20 Linear / Dynamics | ||
|
3.6 MB |
ST7-R3.10.20.1 Modelling a Rotating Body and Centrifugal Load A linear static analysis due to a centrifugal load is performed with Strand7. The analysis is required to determine whether a turning chuck satisfies stress and deformation criteria under rotating operational conditions. The geometry of a turning chuck is provided in the accompanying IGES file. This Webnote outlines the procedure for importing and manipulating the CAD geometry, automeshing, applying non-structural mass to the model, applying a rotational velocity of 3000 RPM about the axis of the chuck, and assigning material properties and characteristics. |

|
|
51.2 MB |
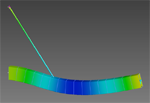
ST7-R3.10.20.2 Harmonic Response Analysis This Webnote introduces the Natural Frequency and Harmonic Response solvers together with some basic concepts in modal analysis. This is done with reference to a simple cantilever beam model, which is harmonically excited at its free end. Ways of introducing damping to the system in Strand7 are then demonstrated, and a comparison is made with a full system transient solution, highlighting the benefits of the modal approach for this type of problem. |
|
|
0.9 MB |
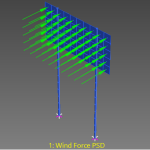
ST7-R3.10.20.3 PSD Analysis of a Wind Load Structures are often subject to loads that fluctuate in a random manner. One such fluctuation is the varying wind pressure acting on a building, caused by the fluctuation in wind speed. Due to the random nature of the wind speed fluctuation, a probabilistic description of the wind speed is most appropriate. This gives rise to the power spectral density (PSD) curves of wind speed. The effect of a given PSD spectrum of wind loading can then be applied to a structure in Strand7 using the Spectral Response solver. This Webnote examines the procedure for applying wind PSD on structures. |
|
|
45.9 MB |
ST7-R3.10.20.4 Harmonic Response of a Rotating Unbalanced Mass In this Webnote, the Harmonic Response and Natural Frequency solvers are used to assess the effect of a rotating force such as normally arises from a rotating out-of-balance mass. This is introduced by a model of a large fan cowling, housing two out-of-balance counter-rotating fans. Rayleigh damping is included in the analysis. |

|
|
1.3 MB |
ST7-R3.10.20.5 Linear Transient Dynamic Analysis The Linear Transient Dynamic solver is used to calculate the time history of the dynamic response of a structure subjected to an arbitrary forcing function and initial conditions; e.g., machinery vibration, wave loading, random earthquake excitation, to name a few. |

|
|
0.6 MB |
ST7-R3.10.20.6 Natural Frequency Analysis with Pre-load The natural frequency of a structure may change due to applied load. This behaviour is exemplified by the classic example of a guitar string, which vibrates at higher frequencies as it is tensioned; the tension stiffens the string in the lateral direction. This Webnote shows how to perform simple natural frequency analysis with and without the pre-load effects. |
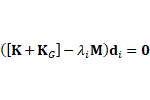
|
|
0.8 MB |
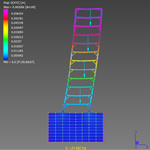
ST7-R3.10.20.7 Using Modal Damping in Harmonic Response Analysis Modal damping is used to include structural damping effects in linear dynamic analysis performed using the mode superposition method (e.g., harmonic response analysis). Each mode included in the mode superposition will have its own frequency, shape and damping ratio. The combination of the modes produces the linear dynamic response of the structure. |
|
|
1.5 MB |
ST7-R3.10.20.9 Spectral Response Analysis In this Webnote, spectral response analysis is discussed as a method for calculating the linear elastic response of a structure under random dynamic loading. This type of loading can be represented using response spectrum or power spectral density (PSD) curves. The excitation applied to the structure may be in the form of base excitation (displacement, velocity, or acceleration) or a dynamic load. |

|
|
1.8 MB |
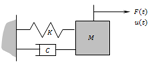
ST7-R3.10.20.10 Modal Mass, Stiffness and the Mass Participation Factor This Webnote discusses the relationships between the following dynamic parameters, and how they can be obtained from Strand7.
|
|
|
4.7 MB |
ST7-R3.10.20.12 Vibrational Analysis of a Wine Glass The harmonic oscillation of a wine glass is a familiar phenomenon to many people. In this Webnote we recreate the harmonic behaviour of a Riedel Vinum Shiraz / Syrah glass. The natural frequency solver is used to recreate the tone generated by rubbing a moistened finger around the rim of the glass, and the linear transient solver is used to recreate the frequency spectrum seen in response to an impulse load. In both cases Strand7 results are compared with experimental results. |

|
|
2.4 MB |
ST7-R3.10.20.13 Response Spectrum and Power Spectral Density This Webnote compares two common techniques of dynamic analysis for stochastic inputs, Spectral analysis with a known Response Spectrum, and Spectral analysis with an input Power Spectral Density, against full transient solutions. |

|
|
0.9 MB |
ST7-R3.10.20.20 Static and Dynamic Stiffness A common transfer function measurement is the Frequency Response Function (FRF). The aim of this Webnote is to give a brief overview of some of these functions, and to take a more detailed look at dynamic stiffness, which is a particular FRF. |

|
|
2.6 MB |
ST7-R3.10.20.22 Compression-Only Footfall Harmonic Response Analysis Footfall analysis on pedestrian-loaded structures is typically done using the Harmonic Response solver to determine the steady-state response to a sinusoidal load. While it's common to apply the peak footfall load, this assumes the load acts in both tension and compression, but in reality, the step load behaves more like a half-sine wave. This assumption isn't necessarily conservative. A discontinuous acceleration from footfall can trigger higher frequency modes, causing harmonics (e.g., 4 Hz, 6 Hz, etc.) beyond the primary footfall frequency of around 2 Hz, which complicates the response. |

|
| << Previous (Overview) | (Nonlinear) Next >> |

 Menu
Menu