|
The linear static solver is the most widely used among the various solvers available.
A linear static solution is obtained assuming that the structure's behaviour is linear
and the loading is static.
|
For the response of a structure to be linear, the mechanical behaviour of all materials
in the model must follow Hooke's law; i.e. element forces are linearly proportional to element deformation and when the loading is removed, the material returns to its original shape. In addition, the deformation must be so small such that the deformed geometry cannot be distinguished from the undeformed one. Because of these two assumptions, solutions can be arbitrarily combined to consider more complex loading conditions. A load is regarded as static if its magnitude and direction do not change with time. Structures under static loading conditions are analysed with the inertial and damping properties ignored.
|
The linear static solver performs the following steps:
|
- Calculates and assembles element stiffness matrices, equivalent element force vectors and external nodal force vectors. In the stiffness calculation, material temperature dependency is considered through the user nominated temperature case. Either consistent or lumped element equivalent load vectors can be calculated according to the option setting. Constraints are also assembled in this process.
At the end of this assembly procedure, the following linear system of equilibrium equations is formed:
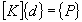
where
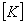 Global stiffness matrix Global stiffness matrix
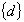 Unknown nodal displacement vector(s) Unknown nodal displacement vector(s)
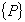 Global nodal load vector(s) Global nodal load vector(s)
- Solves the equations of equilibrium for the unknown nodal displacements.
- Calculates element strains, stresses, stress resultants and strain energy densities as requested.
|
Notes
|
- As the stiffness matrix is independent of the loading conditions, multiple load cases can be considered in one solution execution. At the end of the solution, displacements and other results for all loading cases are calculated.
- If combined loading conditions from the basic load cases are of interest, the post-processor can be used to find the structure's response by simply combining the results for the basic load cases, without running the linear static solver again.
|
For more information on linear static analysis, see Strand7 Webnotes - Linear / Statics.
|

 Menu
Menu