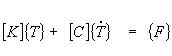Strand7 Software:  In Detail:  Solvers:  Heat Transfer

Strand7 heat solver

Strand7 may be used for the analysis of heat transfer problems. The heat solver in Strand7 supports both linear and nonlinear modes of heat transfer, with either steady-state of transient heat transfer.

Steady state heat solver

The steady state heat solver is used to calculate the temperature distribution in a structure in the steady state or equilibrium condition. The steady state heat solver considers three basic modes of heat transfer: conduction, convection and radiation. The output from the steady state solver is a single value of temperature for each node. Derived values such as flux and temperature gradients are also available.

Two types of steady state heat solutions are possible:

Linear - The linear solver can be used for problems that involve conduction and convection modes of heat transfer and where the material properties are independent of temperature.

Nonlinear - Any problem that includes radiation heat transfer, or temperature dependent material properties, requires the nonlinear solver.


The steady state heat solver performs the following steps:

  • Calculates and assembles the element conductivity matrices and the element and nodal load vectors. The load vectors are derived from the convection and radiation coefficients and the nodal temperatures.

    At the end of this assembly, the following system of equilibrium equations is formed:



    where

    [K] = 'Stiffness' or conductivity matrix
    The use of the word stiffness is a convenient analogy with the structural FEA formulation

    {F} = Applied load vector

    {T} = Vector of nodal temperatures

  • Solves the equations of equilibrium for the unknown nodal temperatures.

  • Calculates the element flux and temperature gradients as requested.

Notes
The solution of a steady state heat analysis, i.e. nodal temperatures, can be used in any of the structural solvers, as a temperature distribution for thermal stress analysis.


Transient heat solver
The transient heat solver uses a time stepping approach to calculate the temperature variation in a structure as a function of time. The solver considers three basic modes of heat transfer: conduction, convection and radiation. The output from this solver is a set of nodal temperatures at each time step. This provides a point wise approximation to the variation of temperature in the structure as a function of time.

Two basic types of transient heat solutions are possible:
Linear - The linear solver can be used for problems that involve conduction and convection modes of heat transfer and where the material properties are independent of temperature, but the temperature varies with time.

Nonlinear - Any problem that includes radiation heat transfer, temperature dependent material properties, or variable time steps, requires the nonlinear solver.

The transient heat solver performs the following steps:

  • Calculates and assembles the element conductivity matrices, the element damping matrices and the element and nodal load vectors. The load vectors are derived from the convection and radiation coefficients and the nodal temperatures. At the end of this assembly, the following system of equilibrium equations is formed:


    where

    [K] = 'Stiffness' or conductivity matrix
    The use of the word stiffness is a convenient analogy with the structural FEA formulation

    [C] = System damping matrix
    {F} = Applied load vector
    {T} = Vector of nodal temperatures
    {} = The rate of change of {T} with time.

  • Solves the equations of equilibrium for the unknown nodal temperatures at each time step.

  • Calculates the element flux and temperature gradients as requested at each time step.

Notes
  1. For linear transient problems where the time step is not constant, the nonlinear solver is required with the damping matrix updated every time the time step changes.

  2. The update of the element stiffness matrices for nonlinear problems can be performed at every step, at every saved step or after a certain number of steps.

  3. The solution at any time step in a transient heat analysis, i.e. nodal temperatures, can be used in any of the structural solvers, as a temperature distribution for thermal stress analysis. The complete thermal transient can be used directly by the nonlinear transient dynamic solver for problems involving time-dependent, thermal stress analysis.

For more information on thermal analysis, see Strand7 Webnotes - Thermal / Heat Transfer.
     About Us  |   Contact Us  |   Sitemap  |   中文（简体）网站
     Copyright  |   Disclaimer