| 瞬态求解器用来计算在力作用或初始条件下结构的时程响应。线性动力平衡方程具有以下形式: |
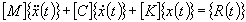 |
式中
|
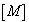 质量矩阵
质量矩阵
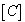 阻尼矩阵 阻尼矩阵
-
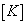 刚度矩阵
刚度矩阵
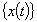 节点位移向量 节点位移向量
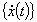 节点速度向量 节点速度向量
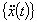 节点加速度向量 节点加速度向量
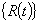 荷载向量 荷载向量
|
对于非线性瞬态求解器,上述内容需要修改以包括非线性对平衡的影响。因为在非线性瞬态求解器中,非线性平衡方程通常在每一个时间步中简化为线性的,这样以下基于上述表达式的讨论仍然是有效的。 |
荷载函数
|
可考虑两种类型的荷载:动力荷载和支座加速度激振荷载:
|
- 模型上的荷载通过荷载因子-时间表来进行放大或缩小。荷载可以随时间任意变化,它可以是节点力、力矩、单元荷载、体积荷载或温度荷载。可以将多种荷载工况合并为一种单一形式的荷载条件。每一种荷载工况可以在求解中考虑或排除,也可按照荷载因子-时间表来放大或缩小。
- 如果在对话窗中选定直接积分,则可考虑多自由度工况。自由度工况中的给定值可象荷载工况的荷载一样进行放缩,从而可使程序考虑随时间而变化的指定位移。
- 模型支座加速度(即带固定自由度的节点)可以用来定义激振。时程可以是任意的,并可在变量—时间表中定义。激振方向可以利用方向向量指定为任意广义坐标的方向。
|
初始条件
|
可以指定以下三种初始条件: |
- 线性静力结果。它指定了结构在某种静荷载作用下的初始位移。
- 一个瞬态分析结果,它确定了结构在某时刻的瞬态反应。求解可以从任何指定的时间步开始。
- 结构中所有自由节点的初始速度和初始加速度。
|
求解技术 |
采用以下两种方法:振型叠加法和直接积分法. |
- 振型叠加法
-
使用振型叠加法,要先求出结构的每个固有振型然后再通过叠加以求得结构的整体响应。这种方法只适用于线性瞬态分析。
- 该方法除振型叠加技术通常的优点之外,它在瞬态动力分析中还有其它的很多优点,其中一个就是除了瑞利阻尼外还可以利用模态阻尼。当有实验数据时,模态阻尼可以更精确地表达系统的阻尼。
- 振型叠加法最适合于动力响应以低频振型为主的结构(如地震)。一般说来,10个振型即可为这些问题提供足够准确的解。振型叠加法不适合于诸如强振或冲击一类的问题,因为在这些问题中存在高频振型。在后一种情况下,可能需要计算直到50次或更高次的振型。而计算如此高的振型的花费足以抵消振型叠加法节省的时间。这一方法的最严重缺点是它不能考虑非线性。
|
-
直接积分法
- 该方法没有振型叠加的缺陷,但由于对所有节点位移在指定时间步上进行数值积分,故计算时间会很长。
|
线性瞬态求解器按以下步骤运行: |
- 根据特定初始条件为节点位移、速度和加速度向量赋初值。
- 对于振型叠加法:计算等效单元荷载向量和组装整体荷载向量。如果考虑支座加速度,则生成整体质量矩阵以计算惯性力项。
-
对于直接积分:计算并组装单元刚度、质量、阻尼矩阵、单元等效荷载向量和整体荷载向量。在刚度计算中,可考虑材料的温度影响;如果包括初始条件,则包括单元的几何刚度矩阵;包括瑞利阻尼和单元材料阻尼。可以选择设定用一致方式还是集中方式形成单元等效荷载向量。约束条件以及规定位移和收缩重复中的常量项也在此过程中施加。单元组装完成后,形成动态平衡方程中的三个整体矩阵,
|
|
|
|
非线性瞬态求解器按以下步骤运行:
|
|
|
注释
|
- 瞬态动力分析的结果是得到某需要时间段内各离散点的一系列解。解的数量和间隔可用时间步控制器来控制。每个时间步上的解包括节点位移、速度和加速度、以及单元应力、应变和其它量。
- 为了确保得到结构的全部反应并保证解的稳定性和收敛,选择正确的时间步长是很重要的。尤其对于非线性解非常重要。
- 一般说来,时间步越短,解越精确。然而,对时间步的长短有一个实用上的限制,因为时间步越小,求解步数就越多,运行时间将显著增加。因此,求解所需要的时间将限制步长不可能太小。时间步的大小还需考虑计算机物理储存器对解文件大小的限制。但是,用Strand7的间断周期存储功能可以取消后一种限制。
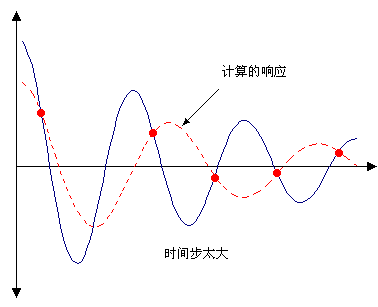
- 如果时间步太大则计算容易漏掉结构的很多高阶频率,如下图所示,从而导致所得到的解不能代表结构的真实行为。
|
 Menu
Menu